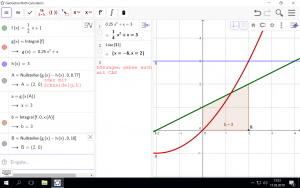
g(x) ist die Stammfunktion/unbestimmtes Integral von f(x), daher ist g(x) gleich der Fläche von 0 bis x unter der Funktion f(x).

Wie man hier sieht, kann man die Grenze auf verschiedene Arten berechnen:

• Man wandelt die Gleichung g(x)=3 in g(x) – 3 = 0 um und lässt die Nullstellen ermitteln.
• Man findet die Schnittpunkte von g(x) und der konstanten Funktion  h(x)=3 (Schnittpunkt roter und blauer Graph).
• man löst g(x)=3 in CAS

… in allen Fällen kommt x=2 heraus (die andere Lösung x=-6 ist meiner Meinung nach nicht gesucht, da b>0 angenommen werden kann).
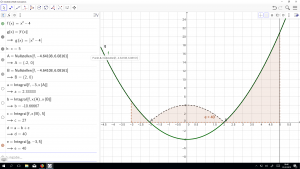
Die Funktionswerte von g(x) sind ja das Integral (=Fläche unter Funktion) von 0 bis x