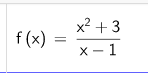Hat man eine rationale Funktion und möchte die Asymptotische Funktion berechnen, so macht man das durch Polynomdivision.
Da wir aber Geogebra zur Verfügung haben, nimmt uns das Programm diese Arbeit ab:

Betrachten wir die folgende Funktion:

die Berechnung muss im CAS-Fenster gemacht werden, im Algebra-Fenster geht es nicht!

CAS:

Achtung: Zähler und Nenner müssen(!) in der Klammer durch einen Beistrich getrennt werden!

Die Ausgabe ist so zu lesen:
Der erste Ausdruck (x+1) ist die Asymptote bzw. Asymptotische Funktion: y(x)=x+1
Der zweite Ausdruck ist der Rest der Division, also 4.
Man kann die Funktion f(x) also auch so schreiben:

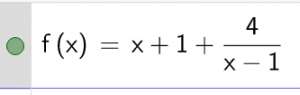
Hinweis: Der Vorgang ist wie bei Division mit Zahlen
14/3 = 4 Rest 2
Daher ist 14/3 = 4+2/3

Beweis (nicht SA-Stoff!):

Wenn man x+1 auf den gemeinsamen Nenner (x-1) bringt (also mit (x-1) erweitert, erhält man:

(x+1)*(x-1)/(x-1)+4/(x-1) =

((x+1)*(x-1)+4)/(x-1)=

(x^2-1+4)/(x-1)=

(x^2+3)/(x-1) … also die ursprüngliche Funktion f(x)