a) ist einfach: den Funktionsterm als Funktion von x (statt  t) eingeben und dann v(12) und v(30) berechnen lassen:

b) Die Winkelgeschwindigkeit (=Kreisfrequenz) ist direkt aus dem Term herauszulesen (Faktor im(!) sin, welcher bei x bzw. t steht).
Daraus kann man die Frequenz pro Sekunde und Minute und die Periodendauer berechnen:

c) Die maximale Atemgeschwindigkeit kann man

• sich durch den Befehl Extremum anzeigen lassen … allerdings steht in der Angabe berechnen!
  Um eine Kontrolle zu haben, ist es jedenfalls zulässig, auch bei der SA diesen Befehl zu verwenden:
  
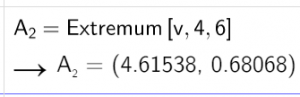
  4 und 6 sind das Intervall, wo ein Extremum drinnen liegt … sonst bekommt man eventuell sehr viele Ausgaben, da ja die Funktion periodisch ist.
  wir bekommen also den x- und den y-Wert (bzw. den t- und den y-Wert)
  Da der y-Wert von v(t) die Geschwindigkeit ist, lautet die Antwort: Die höchste Geschwindigkeit beträgt 0,68068 l/s.
• Um den Wert zu berechnen, muss man nur die Amplitude (also der Faktor vor dem sin) angeben:
  

d) Die erste Nullstelle muss man mit dem Term im sin berechnen, da ja sowohl die Winkelgeschwindigkeit, als auch die Verschiebung die Nullstelle beeinflusst:
Man weiß, dass sin(0)=0 und sin(pi)=0. Man kann somit den Term im sin =0 bzw. =pi setzen und damit die Nullstellen berechnen:
bzw. dezimal: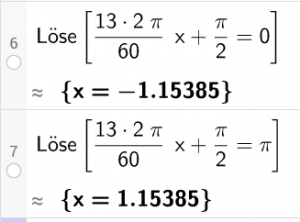

Da mit erster Nullstelle aus dem Textkontext eher „erste Nullstelle > 0“ gemeint ist (siehe Graphik im Buch), ist nach 15/13 = ca. 1,15385 sek. die richtige Antwort.

Die Bedeutung der Nullstelle: Da v(t) die Atem-Geschwindigkeit angibt, welche zwischen positiven und negativen Werten wechselt (Ein- bzw. Ausatmen … je nachdem, was man als positive Geschwindigkeit sicht auch umgekehrt), muss man sich überlegen, wann beim Atmen die Geschwindigkeit 0 ist – das passiert genau zwischen Ein- und Ausatmen, dort, wo man eben vom Ein- zum Ausatmen wechselt bzw. umgekehrt.

e) Die Lösungen sind:

Die Frequenz von v(t) ist größer als von f(t) … die Sinusfunktion hat ja die Frequenz von 1/(2*pi):

daher stimmt B.

Da die Amplitude von v(t) kleiner als 1 ist, handelt es sich um eine Stauchung (C) und nicht um eine Streckung(A).

Da die Frequenz von v größer ist, ist die kleinste Periode kleiner als die von f(t), welche ja 2*pi ist. D stimmt daher nicht:

Da, wie bereits gesagt, die kleinste Periode von v(t) kleiner als die von f(t) ist, kann sie nicht 2*pi sein (das ist ja die Periode von f(t)):

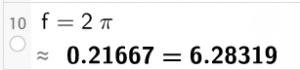
E ist somit falsch.