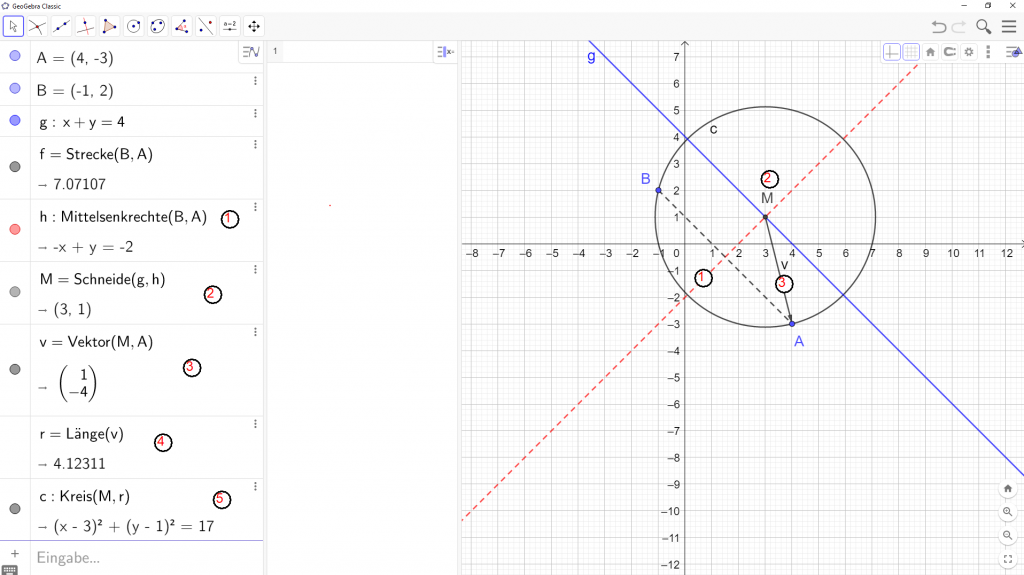
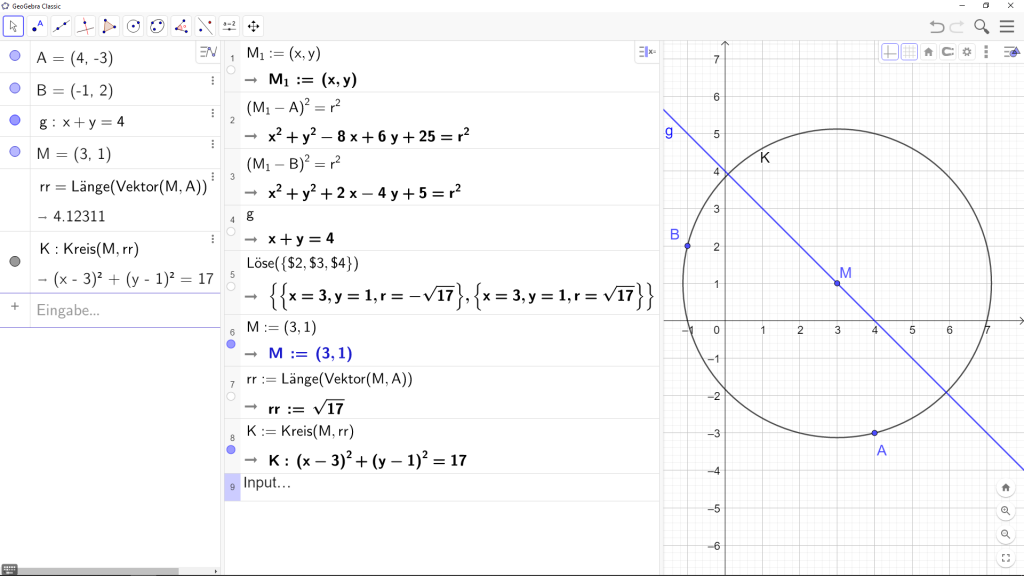
Kreisbestimmung (2 Punke, Gerade durch M)

Ein Kreis soll durch die Punkte A und B gehen und der Mittelpunkt soll auf der Geraden g liegen.

Unbekannt: Mittelpunktskoordinaten, Radius

A = ( 4 | -3 )
B = ( -1 | 2 )
g: x + y = 4

Geogebra Algebra

Die Punkte A, B und die Gerade g werden wie gewohnt eingegeben.

Die Strecke f ist nicht für die Lösung relevant, sondern dient nur der Veranschaulichung (da darauf die Streckensymmetrale = Mittelsenkrechte h gebildet wird)

  1. Der gesuchte Mittelpunkt M des Kreises muss von A und B denselben Abstand (r, noch unbekannt) haben.
    Daher muss der Mittelpunkt auf der Streckensymmetralen h liegen (Geogebra verwendet den Begriff/Befehl Mittelsenkrechte).
  2. M ist der Schnittpunkt von g und h.
  3. Die Länge des Vektors MA (es würde auch MB funktionieren) ist der Radius r.
  4. Der Kreis ist somit mit M und r aufstellbar.

Geogebra CAS

  1. Der Mittelpunkt M1 wird mit den Koordinaten x und y definiert.
  2. Mit der Vektorform lassen sich dann leicht durch Einsetzen der Punkte die ersten 2 Gleichungen $2 und $3 aufstellen.
  3. Die Gleichung der Geraden $4 vervollständigt das 3×3-Gleichungssystem
  4. Durch Lösen des Gleichungssystems in $5 erhält man 2 Lösungen, wobei die Lösung mit negativem r zu verwerfen ist.
  5. Die Definition von M und die Berechnung des Radius (Abstand MA = Vektorlänge MA) sind die letzen Schritte und der Kreis kann in $8 aufgestellt werden.