
Die Kostenfunktion K(x) kann in GG dargestellt werden.
Die Stückkostenfunktion ist K(x)/x und kann ebenfalls dargestellt werden und das verlangte Minimum mit dem Befehl „Extremum“ gefunden werden.
Nicht vergessen K“ muss >0 sein (Achtung! Ist erst in der 6. Nachkommastelle ungleich 0, daher bei Runden auf weniger Stellen wird 0 angezeigt! Die Abfrage mit >0 ist sicherer – Alternative: mehr Nachkommastellen anzeigen)
(die Lösungen für x=0 sind uninteressant und „seltsam“, da für x = 0 gleich zwei Lösungen gefunden wurden, was eigentlich nicht möglich ist).
Hier wurde die Stückkostenfunktion noch mit einem Faktor 100 multipliziert, um beide Funktionen in einem Graphen darzustellen:
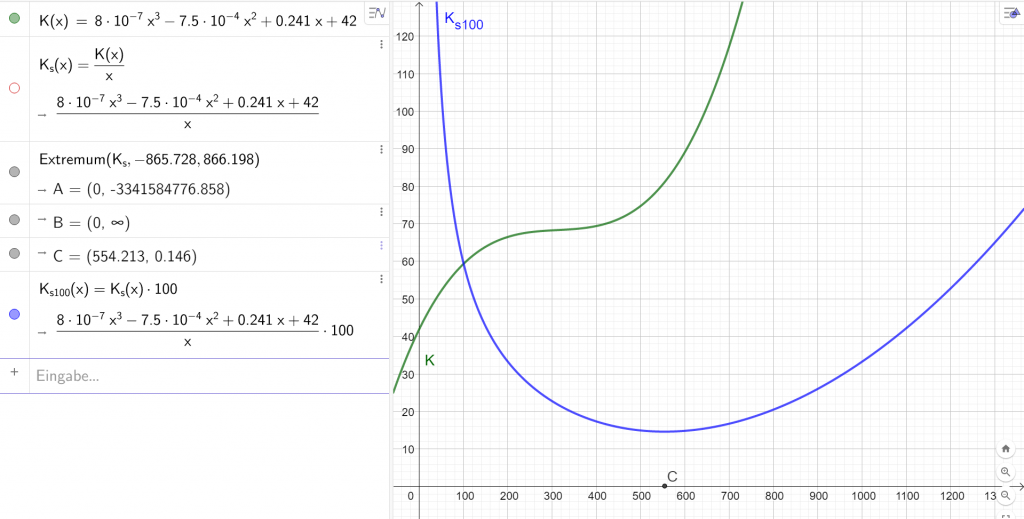
Das Betriebsoptimum zur Kostenfunktion x_opt liegt also bei ca. 554 Stück.
Um die (Gesamt-)Kosten für diese Menge zu berechnen, ermittelt man K(x_opt) = K(554) = K(x(C)) = ca. 81,11 GE.
Diese Kosten machen p=65% seines verfügbaren Kapitals aus, daher ist 81,11 der Anteil einer Prozentrechnungsgleichung G = A/p.
Man erhält für G = 124,78 GE. Das ist also das zur Verfügung stehende Kapital.
Hier gehts zu 2_052d