Grundlagen

Ereignisse, die im Baum unterhalb eines anderen Ereinisses liegen, sind immer „unter der Bedingung“ der darüberliegenden Ereignisse zu sehen.
Manchmal hat das keine Auswirkung auf das Ereignis (z.B. bei „mit Zurücklegen“), manchmal schon (z.B. bei „ohne Zurücklegen“).
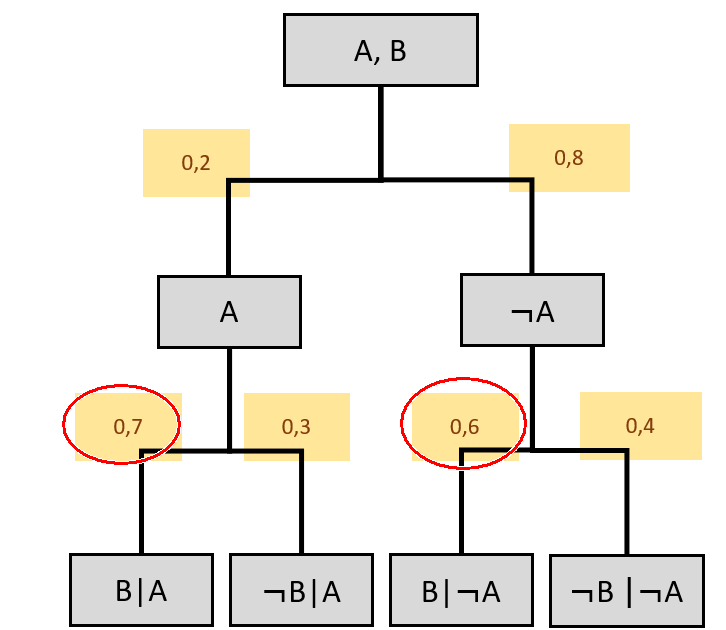
Hier ist 0,7 nicht gleich 0,6.
„A“ bzw. „nicht A“ hat eine Auswirkung auf B, wenn B darauf folgt.
Die Wahrscheinlichkeiten innerhalb einer Verzweigung ergänzen sich auf 1:
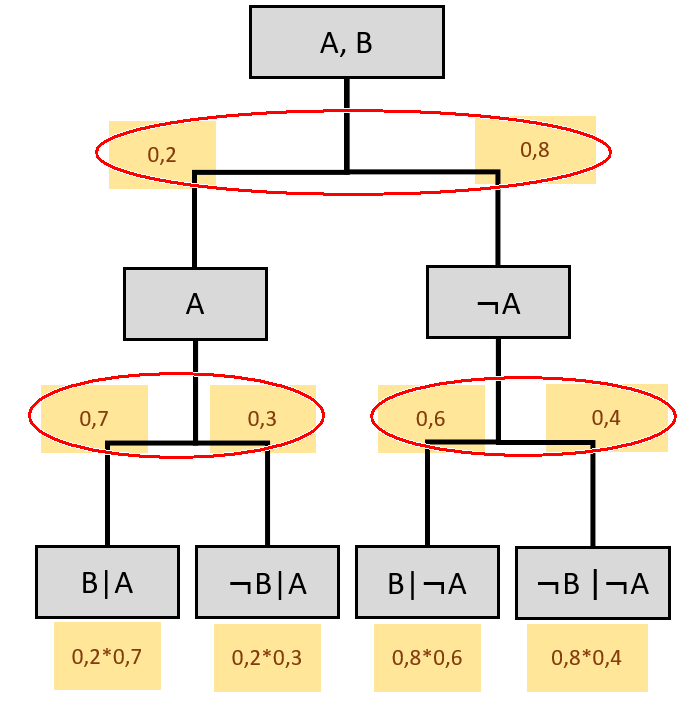
Die Summe aller Pfadwahrscheinlichkeiten ergibt ebenfalls 1.
Es müssen aber alle möglichen Pfade angeschrieben sein, der Baum also vollständig sein!
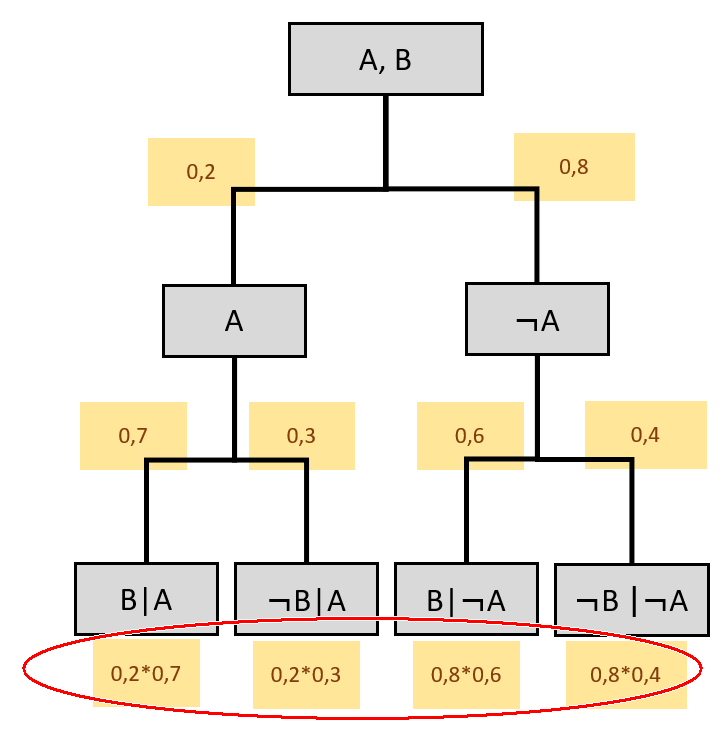
Bedingte Wahrscheinlichkeit
Die Pfadwahrscheinlichkeiten sind in der Vierfeldertafel in der Mitte zu finden:
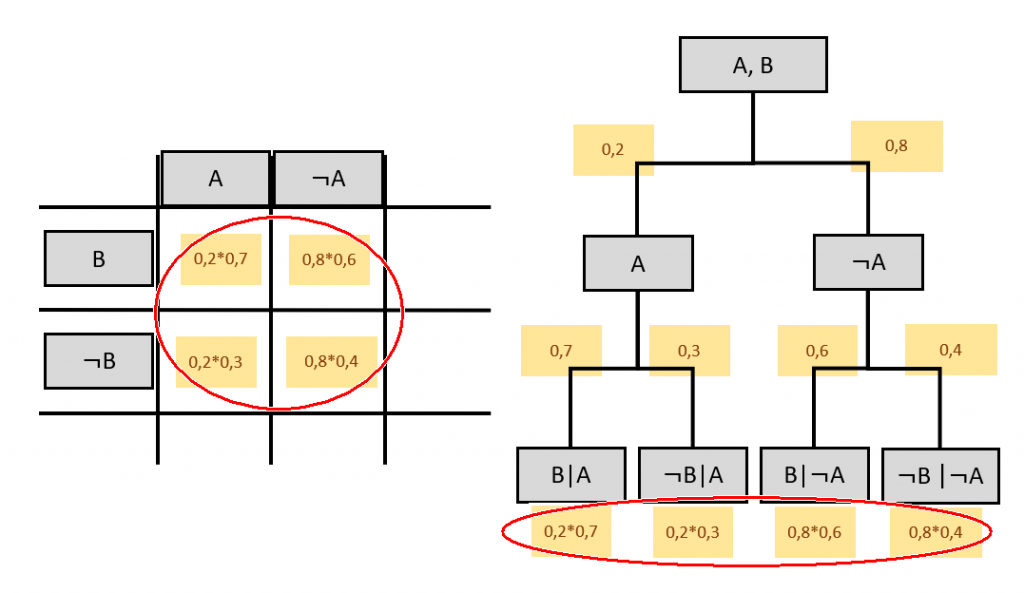
Die Elementarwahrscheinlichkeiten der ersten Stufe sind außen zu finden.
Ein Ereignisbaum gibt nur die 2 dieser vier Werte direkt aus:
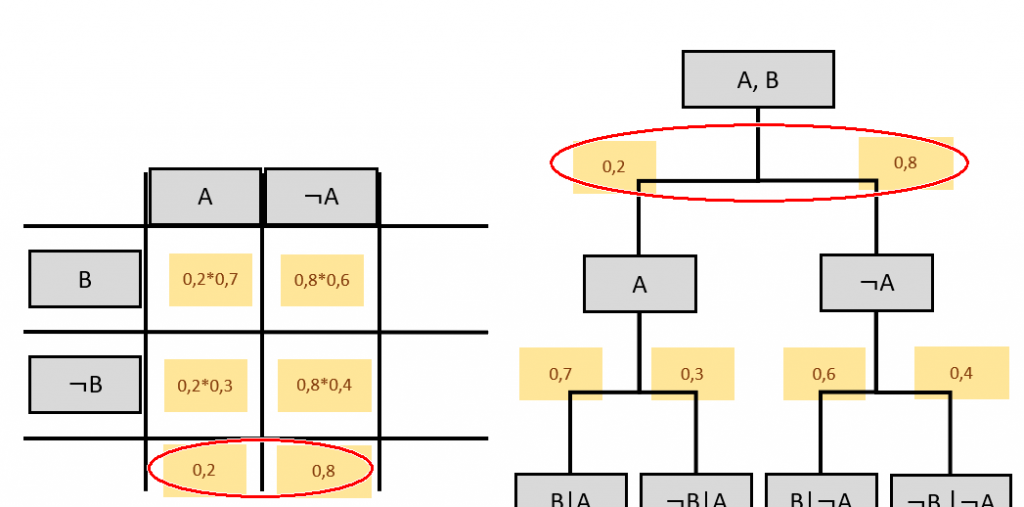
Die beiden anderen Wahrscheinlichkeiten können als Zeilensumme (oder Spaltensumme, falls die Tabelle anders herum angelegt worden ist) berechnet werden:

Ergebnis:
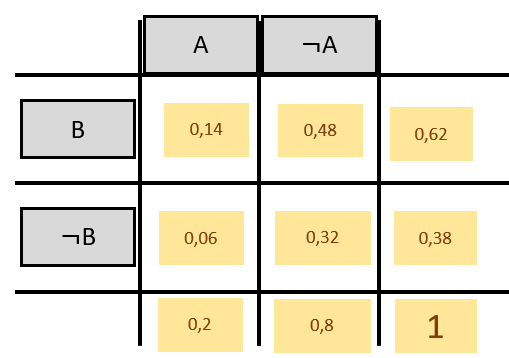
Variationen, Kontrollen und Abkürzungen
Ist die Vierfeldertafel nicht mit Wahrscheinlichkeiten gefüllt, sondern mit absoluten Zahlen, muss man jede Zahl durch die Gesamtsumme dividieren, um die Wahrscheinlichkeitstafel zu bekommen:
Dividiere alle Werte durch 2000 und du erhältst die obige Tafel!
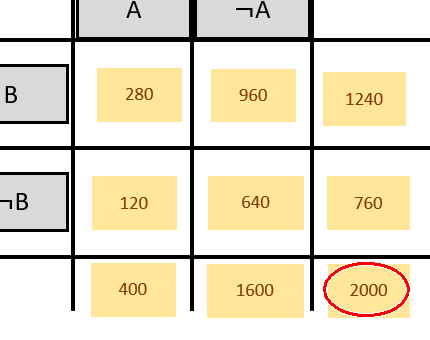
Da sich die eingekreisten Felder jeweils auf 1 ergänzen, kann man einen fehlenden Wert oft als Gegenwahrscheinlichkeit berechnen:

Wahrscheinlichkeiten 2. Stufe
Woher bekommt man nun die Wahrscheinlichkeiten der 2. Stufe?

Wenn du hinaufscrollst, siehst du, dass diese Wahrscheinlichkeiten beim Aufstellen der Vierfeldertafel NICHT verwendet wurden, daher kannst du sie umgekehrt auch nicht auslesen.
Nennen wir eine dieser gesuchten Wahrscheinlichkeiten p.
p ist hier P(nicht A|B).
Da die Pfadwahrscheinlichkeit durch Multiplikation entlang des Pfades berechnet werden kann, muss also 0,62*p = 0,48 ergeben.
Somit ist p = 0,48/0,62 = ca. 0,7742
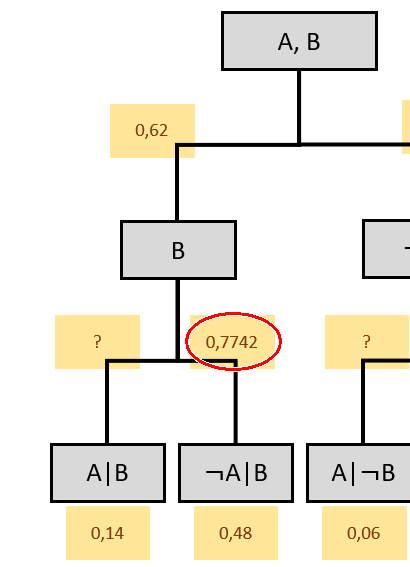
die restlichen Wahrscheinlichkeiten können auf die gleiche Weise und teilweise mit Gegenwahrscheinlichkeit berechnet werden (zur Erinnerung: Verzweigungen ergänzen sich auf 1).
In der Vierfeldertafel wird ebenfalls dividiert:
Es ist genau die selbe Rechnung!
P(nicht A|B) = 0,48/0,62 = ca. 0,7742

Hier funktioniert es auch mit Absolutzahlen:
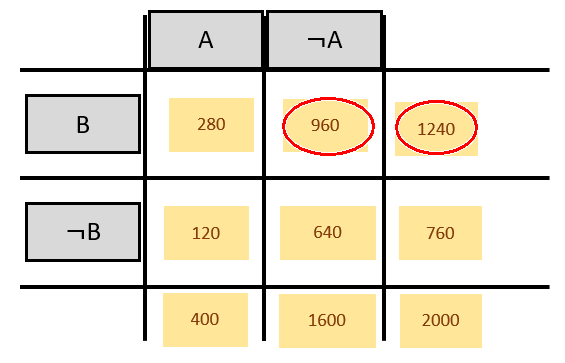
P(nicht A|B) = 960/1240 = ca. 0,7742