918
Es werden zwei Würfel geworfen und die folgenden Ereignisse definiert:
E1: Die beiden Augenzahlen sind gerade.
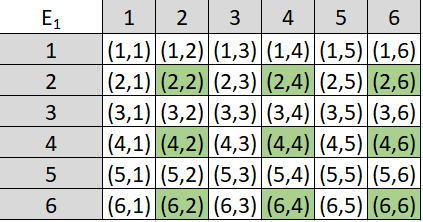
SÜ M1e 16.9.2020 „Dezimalzahlen“
Histogramm
Histogramme sind eine etwas speziellere statistische Darstellungsform.
Die waagrechte Achse (Abszisse) muss sich auf metrische Werte beziehen (also auf einer Skala abbildbar sein, die gleiche, definierte Abstände hat).
Das ist deshalb wichtig, weil die Intervallbreite (=Breite der Säule) eine mathematische Bedeutung hat!
Eine Notenskala wäre z.B. nicht sinnvoll!
Die Breiten der Säulen können unterschiedlich sein!
Die Anzahl der Daten, die in das jeweilige Intervall fallen, werden als FLÄCHEN! der einzelnen Säulen dargestellt:
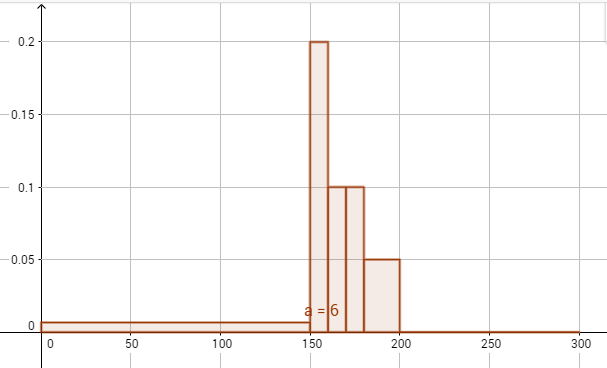
Wie liest man nun die Daten in so einem Histogramm?
Da absolute Häufigkeit mit den Flächen gleichgesetzt sind, und Rechtecksflächeninhalte mit Länge*Breite berechet werden, also A = h*b, ergibt sich für die Höhe der Säulen h=A/b.
Daher muss die absolute Anzahl durch die Intervallbreite dividiert werden, um die Höhe der Säule zu erhalten!
Wenn man das obige Diagramm betrachtet, so hat zum Beispiel die Säule für [180;200[ eine Breite von 200-180=20 und die Höhe =0,05.
Fläche ist demnach 20*0,05=1, somit gibt es 1 Wert in diesem Intervall.
Den genauen Wert kann man nicht bestimmen, er könnte also 180 oder auch 197 sein.
Die Höhe der Säulen interpretiert man als Häufigkeitsdichte, sie gibt also eine Übersicht, in welchen Intervallen die Werte dichter vorkommen als in einem anderen Intervall.
Der Geogebra-Befehl „Histogramm“setzt sich aus 2 Datenmengen zusammen:
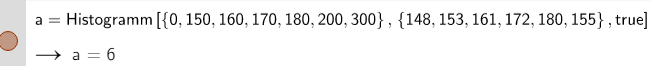
Die erste Menge beinhaltet die Grenzen der Intervalle, es werden hier mit den 7 Werten also 6 Intervalle definiert.
Die zweite Menge beinhaltet die Datenwerte. Diese werden dann in die jeweiligen Intervalle automatisch eingerechnet.
Die Datenwerte im Diagramm sind dann die ANZAHLEN, wie viele Werte im Intervall vorkommen.
Der Wert „true“ gibt die absolute Häufigkeit als Fläche, „false“ gibt die absolute Häufigkeit als Höhe aus, was eine eher unübliche Darstellung ist.
Muss man die Höhe händisch berechnen, so müsste man zuerst eine Klasseneinteilung machen:
[0;150[ : 148 also absolute Häufigkeit = 1 (EIN Wert im Intervall)
[150;160[ : 153, 155 -> 2
[160;170[ : 161 -> 1
[170;180[ : 172 -> 1
[180;200[ : 180 -> 1
[200;300[ : kein Wert -> 0
Demnach sind die Höhen = absolute Häufgigkeit dividiert durch Intervallbreite:
1/150 = 0,006666…
2/10 = 0,2
1/10 = 0,1
1/10 = 0,1
1/20 = 0,05
0/100 = 0
Menge der natürlichen Zahlen
Schulbuchausgabe 2020/21
Stoff WH-Prüfung Mathematik 2f
Prüfungstermin September 2020
Teilbarkeit natürlicher Zahlen
Teiler und Vielfache
Schreibweisen – Teilermengen/Vielfachmengen – Komplementärteiler – echte und unechte Teiler – Primzahlen – Primfaktorenzerlegung, ggT, kgV – Summenregel/Differenzenregel/Produktregel für Teilbarkeit – Teilbarkeitsregeln für 2, 3, 4, 5, 9, 10 – Textaufgaben
Symmetrie, Koordinatensystem, Winkel, Dreiecke
Zeichnen/Ablesen im Koordinatensystem – Strecken/Seitensymmetrale – Winkelsymmetrale, Höhe, Schwerlinie – U, I, H, S im Dreieck – kongruente Figuren – Spiegeln von Figuren – supplementäre und kompementäre Winkel – Parallelwinkel und Normalwinkel – Z-Regel – Arten von Dreiecken, Konstruktion von Dreiecken – Beweis/Anwendung Winkelsumme – Flächenberechnung rechtwinkelige Dreiecke und zusammengesetzte Figuren (Dreiecke/Rechtecke) – Maßstab und Einheiten (Länge u. Fläche, Zeichnen) – Textaufgaben
Brüche und Prozentrechnung
Defintion von echter, unechter, uneigentlicher Bruch – Kürzen und Erweitern von Brüchen – Brüche auf gleichen Nenner bringen können – Dezimalzahlen in Brüche umwandeln – Brüche in Dezimalzahlen umwandeln – Rechnen mit Bruchtermen (inkl. Klammerausdrücke) – Prozentrechnungsformel (p, A, G) anwenden können – Prozent und Promille – Textaufgaben
Gleichungen
Gleichungen lösen (Umformen/Umkehroperationen!, nicht graphisch, nicht im Kopf!) – Probe – Textaufgaben
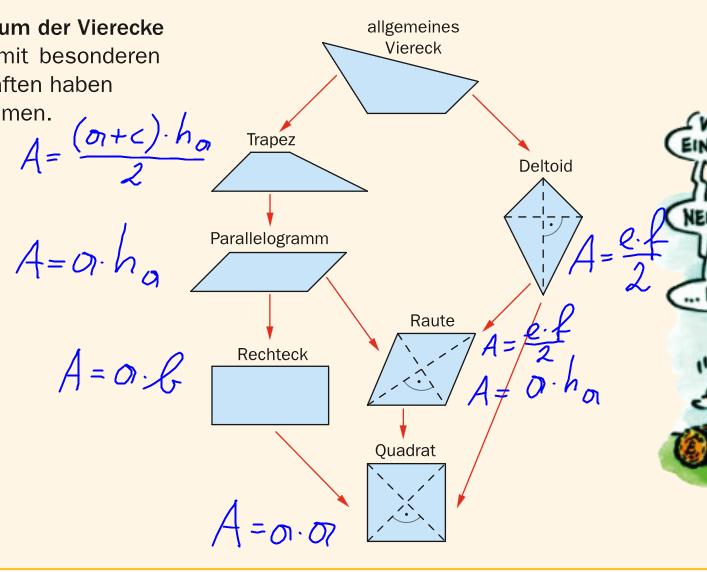
Vierecke
Eigenschaften von Vierecken (Seiten, Diagonalen, Winkel, Inkreis, Umkreis)
keine Konstruktionen!
Direkte und indirekte Proportionalität
Eigenschaften – Erkennen/Überprüfen ob eine Proportionalität vorliegt (Tabelle und Graph) – Graph zeichnen können – Textaufgaben