Beispiel 690
Geogebra-Datei: Hangneigung Schistöcke (Zip-Datei, 20KB)
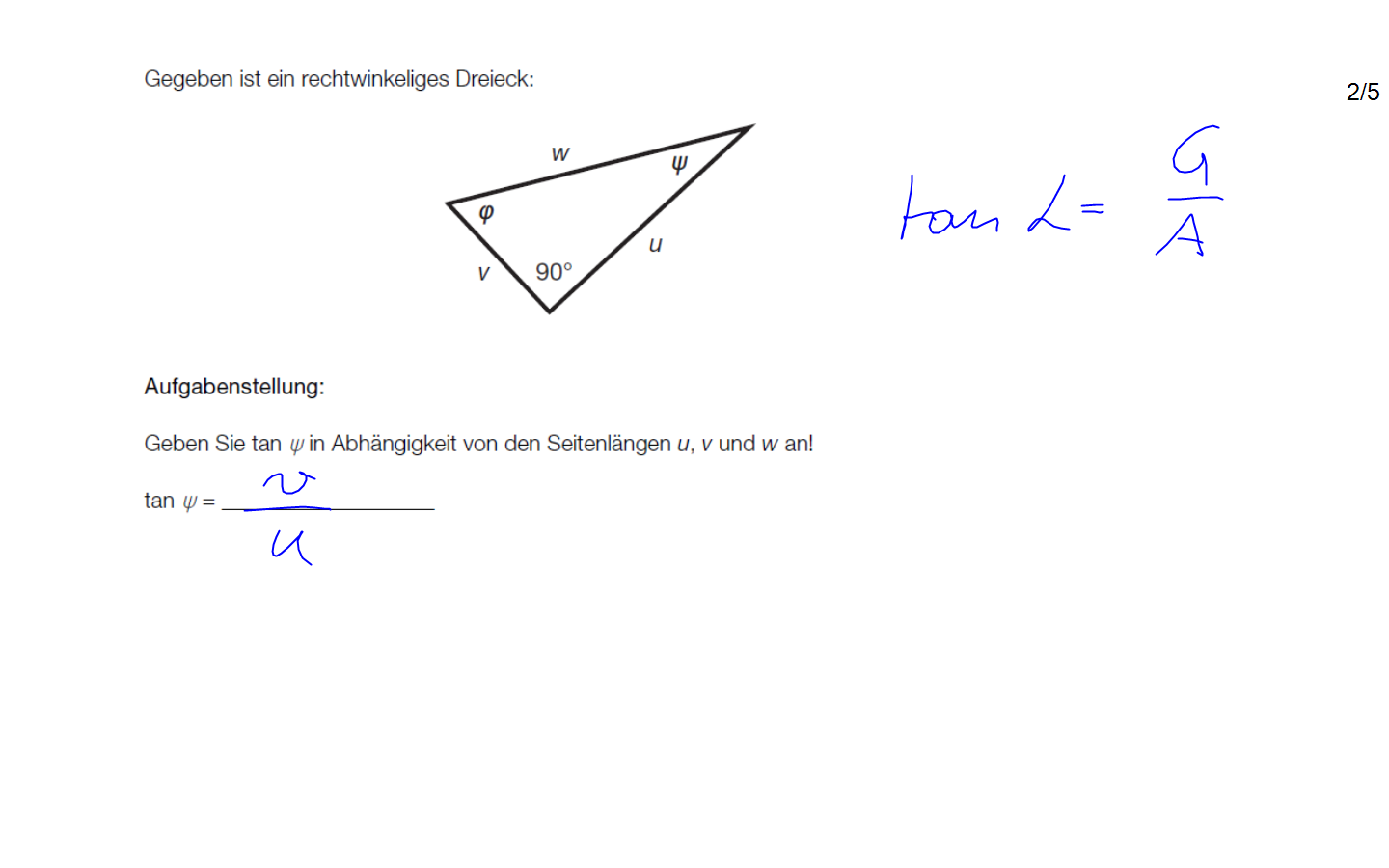
Ein Beispiel, das zwar interessant ist, aber das SchülerInnen immer Probleme macht.
Vorstellung und Durchführung in der Realität:
Man steht als Schifahrer auf dem Hang und macht auf dem Hang in Falllinie einen Abdruck des Schistocks in den Schnee.
Dann sticht man einen Schistock am oberen Abdruckpunkt ein, hält den zweiten Stecken zum Griff des ersten und lässt diesen zweiten Schistock nach unten pendeln.
Dann neigt man den ersten Schistock so weit hangabwärts, bis die Spitze des zweiten Schistocks den Schnee berührt.
Es gibt dann 3 Fälle:
- Der senkrechte Schistock sticht innerhalb des Abdrucks in den Schnee ein (flache Hangneigung < 30°):

- Der senkrechte Schistock sticht unterhalb des Abdrucks in den Schnee ein (steile Hangneigung >30°):

- Der senkrechte Schistock sticht genau am Ende des Abdrucks in den Schnee ein (Hangneigung = 30°):

Betrachtet man nun diese letzte Graphik, dann sieht man folgende Zusammenhänge:
- der Abdruck des Schistocks und die beiden Schistöcke bilden ein gleichseitiges Dreieck
- da auch alle Winkel gleich groß sind sind alle Dreieckswinkel 60° (180°/3)
- die Waagrechte vom oberen Abdruckendpunkt ist eine Höhe dieses Dreiecks.
Da das Dreieck symmetrisch ist, teilt diese Höhe auch den Dreieckswinkel von 60° in 2 gleich große Winkel zu je 30°.
Somit haben wir gezeigt, dass mit dieser Methode genau ein 30° Winkel ermittelt werden kann.