Ereignisbaum zeichnen (jeden Zweig immer nur so weit, bis die erste Dame aufgedeckt wird) und dann Erwartungswert wie in Lösung berechnen.
Pool 1_635
- JA, weil symmetrisch
- NEIN, weil Y-Werte weiter „draußen“
- JA, weil 0,1+0,5 < 0,1+0,2
- NEIN, weil 0,1+0,2+0,3+0,2+0,1 ungleich 0,2+0,15+0,1+0,15+0,2 ist
- NIEN, weil 0,05+0,1+0,2+0,3 > 0,3
Richtiges Ankreuzen (SA, Matura, …)
Pool 1_544
Pool 1_611
Hier ist ein Beispiel, wo man nicht blind drauflos rechnen sollte.
Rechnen kann man hier auch nicht viel (es steht NICHT da, dass es sich um eine Binomialverteilung oder ähnliches handelt, daher sind die restlichen Wahrscheinlichkeiten gar nicht berechenbar!)
M81 – Schularbeitsstoff
Für genauere Beschreibungen siehe Grundkompetenzenkatalog im Downloadbereich
Als Übungsbeispiele bieten sich die entsprechenden Beispiele im Aufgabenpool und in den Schulbüchern an.
FA2: Lineare Funktionen
AN1 bis AN4: Analysis
WS1: Beschreibende Statistik
WS2: Wahrscheinlichkeitsrechnung
WS3.1 bis WS3.3: Wahrscheinlichkeitsverteilung(en)
ohne WS3.4
M71 – Umkehraufgabe
Pool 1_403
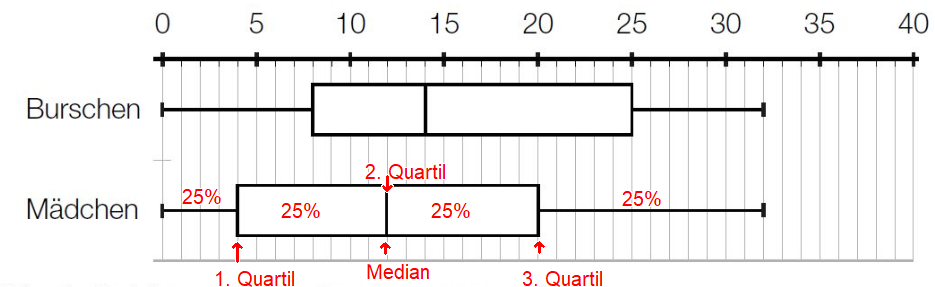
Boxplot: Quartile, Median
Quartile teilen die Werte in 25%-Blöcke ein, wobei der Median dem 2. Quartil gleichgesetzt wird.
M8typ – Dreieck in Ellipse
Bestimme das flächengrößte gleichschenkelige Dreieck, welches in der Ellipse mit a=5, b=3 liegt und dessen Spitze in (0 ; -b/2) und die beiden anderen Eckpunkte auf der Ellipse liegen (symmetrisch zur y-Achse).

HB: Fläche: 2x (y+3/2)*1/2 (Seite*Höhe*1/2)
NB: Ellipsengleichung

Es muss nun nur noch $2 als Funktion definiert werden und das Maximum gesucht werden.