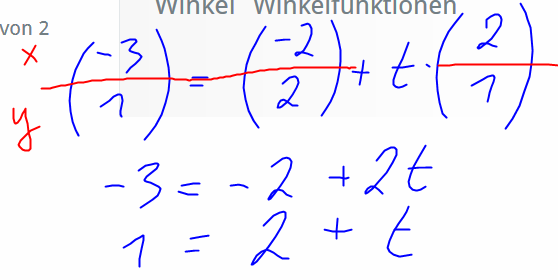Gegeben ist der Punkt A (-3|1) und die Gerade g: X = (-2|2) + t(2|1).

Gesucht ist der Parameterwert von t, der den Punkt A ergibt.

Da X ein allgemeiner Punkt der Geraden ist, kann auch A dort eingesetzt werden:

(-3|1) = (-2|2) + t(2|1)

Man kann nun die x-Zeile und die y-Zeile untereinander als Gleichungssystem von 2 Gleichungen (mit 1 Variablen t) anschreiben:

I: -3 = -2 + 2t
II: 1 = 2 + t

Löst man nun eine der beiden Gleichungen, erhält man einen Wert für t:

Nehmen wir mal die Gleichung I. Man erhält t = -1/2 = -0,5.

Jetzt haben wir aber noch Gleichung II! Auch für diese muss dieses t gelten um den Punkt A zu erhalten.
Setzt man jedoch t in II ein erhält man eine falsche Aussage – oder man berechnet t aus der Gleichung II und erhält einen anderen Wert (hier t = -1) … jedenfalls passt irgendetwas nicht.

Interpretation: Es gibt eben KEIN t, für das beide Gleichungen gelten. Man könnte auch sagen, es gibt keinen Parameter t, mit dem man den Punkt A erreicht.
Da aber mit der Parameterdarstellung ALLE Punkte einer Geraden erreicht werden können, kann man folgern, dass A nicht auf g liegt.

Es gibt als keine t und daher ist die Aufgabe auch nicht lösbar.