Um die Winkelsymmetrale zu berechnen, benötigt man zuerst die Richtungsvektoren der Ausgangsgeraden g und h.
Der Richtungsvektor der Winkelsymmetrale wird durch Vektoraddition zweier gleich langer Richtungsvektoren von g und h  … also g+h aufgebaut.

Warum müssen die Vektoren gleich lang sein?
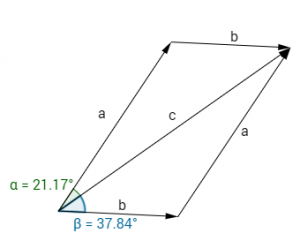
Weil nur bei einer Raute die Diagonale auch Winkelhalbierende der Seiten ist (beim Parallelogramm ist das nicht der Fall)
Bei der Addition von zwei Vektoren ist aber nur ein Parallelogramm (z.B.: Kräfteparallelogramm) vorhanden und daher bekommt man im Normalfall eben auch keine Winkelsymmetrale.

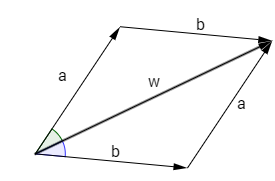
Ändert man jedoch die Länge eines Vektors so, dass er gleich lang wie der andere Vektor wird – oder bringt beide Vektoren auf die selbe Länge (z.B.: Einheitsvektoren) erhält man eine Raute und die Summe der beiden (gleich langen) Vektoren ergeben einen Vektor w in Richtung der Winkelsymmetralen:

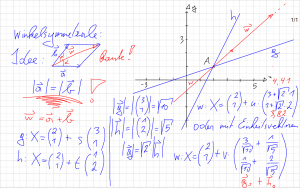
Vektor g hat die Länge Wurzel(10), Vektor h hat die Länge Wurzel(5) … daher ist Faktor Wurzel(2), um den Vektor h auf die Länge von Vektor g zu bringen.

Man erhält dann durch Addition von Vektor g und Wurzel(2)*Vektor h den Vektor (4,41 | 3,82), der schon in Richtung der Winkelsymmetralen zeigt.

Die andere Möglichkeit ist das Aufstellen von den beiden Einheitsvektoren von g und h, was in der unteren Geradengleichung von w gemacht worden ist.
Man erhält dann einen kürzeren Richtungsvektor von w.

Auf Grund der Wurzel (Längenberechnungen mit Pythagoras) sind in der Regel leider keine schönen Werte zu erwarten.