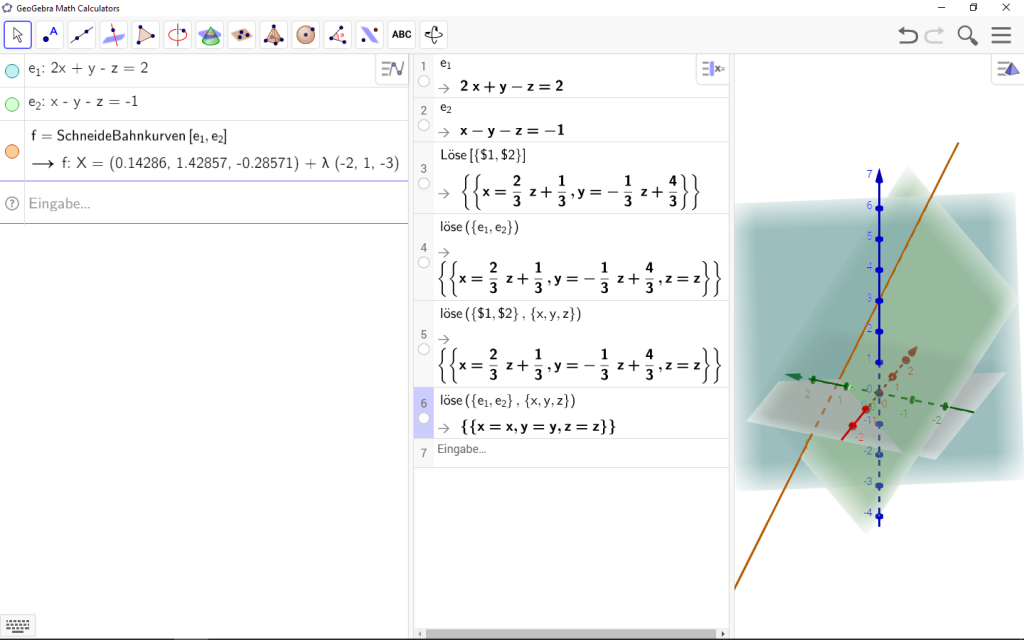
Im folgenden Screenshot werden 2 Ebenen geschnitten.

Da hier 2 Gleichungen (e1, e2) und 3 Variablen (x,y,z) vorhanden sind, haben wir einen Freiheitsgrad.
Das bedeutet, dass eine Koordinate (bzw. ein Parameter) frei wählbar ist … somit ist das Ergebnis im Normalfall eine Gerade.

Wie löst man dieses Gleichungssystem:

• Möchte man die Gleichungen als Ebenen auffassen, so schneidet man im Algebra-Fenster (in der Graphik links)
  Es ist nicht norwendig „SchneideBahnkurven“ einzugeben, das macht Geogebra nach der Eingabe von „Schneide(e1,e2)“ selber.
  Die Ausgabe ist die Gerade f , wobei oft die Zahlen nicht wirklich schön sind, daher genug Stellen anzeigen lassen!
• In CAS kann man verschiedene Eingaben machen: $3 bis $5 geben sinnvolle Lösungen, $6 seltsamerweise nicht.
  Hinweis: die Einfachere Variante wählen, also keine Lösungsvariablen angeben.
  Wichtig: die Gleichungen (bzw. die Gleichungsnamen oder CAS-Zeilennummern) in eine Geschwungene Klammer {} geben!
  Hier sieht man deutlich den Freiheitsgrad (hier ist z beliebig „z=z„) für die Lösungspunkte (Gerade ist ja eine Punktmenge)