Einige Tipps und kleine Merksätze für die 2. SA

• Krümmung positiv = Stimmung positiv = Smiley, Krümmung negativ = Stimmung negativ = Bady
• Steigung in einem Punkt = Steigung der Tangente
• Ist zwischen zwei Extremstellen genau eine Wendestelle, ist dort die Steigung betragsmäßig am größten
• Polynomfunktionen haben keine undefinierten Stellen/Polstellen:  D=R
• Nur gerade Polynomfunktionen können keine Nullstelle haben … ungerade Polynome müssen mindestens eine Nullstelle haben.
• Gewinnschwelle (Break-Even-Point) ist vor Gewinngrenze:
  dazu die Eselsbrücke: Zuerst muss ich meine Wohnungsschwelle übertreten, bevor ich über die (Stadt/Landes)grenze treten kann.
• Ist die Ableitung f‘ ein Polynom n-ten Grades, muss die Funktion f ein Polynom (n+1)-ten Grades sein (also ein Grad höher)
  Ist die Ableitung ein Polynom 2. Grades, ist die Funktion ein Polynom 3. Grades
• Ist die 2. Ableitung f“ eines Polynom n-ten Grades, muss die Funktion ein Polynom (n+2)-ten Grades und die Ableitung f‘ ein Polynom (n+1)-ten Grades sein.
  Ist die 2. Ableitung f“ ein Polynom 1. Grades (lineare Funktion), so muss die Funktion ein Polynom 3. Grades und die Ableitung eine quadratische Funktion sein.
• Bei Extremwertaufgaben die Hauptfunktion finden … diese Fragen sollte man sich dabei stellen:
  • Was soll maximiert/minimiert werden?
  • welche Einheit hat das?
  • wie berechnet man es?
• Asymptoten der Form y=kx+d bzw. die asymptotische Funktion berechnet man mit Geogebra, indem man den Zähler durch den Nenner dividiert:
  Die Funktion:
  
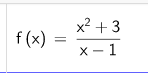
  Die Eingabe und das Ergebnis:
  im CAS-Fenster!!!
  
  Die Interpretation:
  Asymptote: y(x)=x+1
  Der Rest ist 4, kann für große x vernachlässigt werden.
  Siehe auch M71 – Asymptoten der Form y=kx+d mit Geogebra
• Bei bestimmten Textbeispielen werden große Werte verwendet … dass man dann im Graphik-Fenster die Funktion nicht gleich sieht, ist klar! Daher: Zoomen!!!
• Wie zeigt man, dass die Steigung in einem Bereich pos./neg. ist?
  • Man unterteilt den Definitionsbereich in Bereiche, in denen sich die Steigung nicht ändern kann:
    Die Grenzen sind Extremstellen und undefinierte Stellen (undef. Stellen sind aber nicht relevant für Polynomfunktionen)
  • Daher ist zwischen zwei Extremstellen die Steigung immer entweder positiv oder negativ … einfach einen beliebigen Wert aus diesem Bereich nehmen und f'(x) ausrechnen (lassen) oder
    von einem Minimum zu einem Maximum kann die Steigung nur positiv sein- von Maximum zu Minimum nur negativ.
• Wie zeigt man, dass die Krümmung in einem Bereich pos./neg. ist?
  • Man unterteilt den Definitionsbereich in Bereiche, in denen sich die Krümmung nicht ändern kann:
    Die Grenzen sind Wendestellen und undefinierte Stellen (undef. Stellen sind aber nicht relevant für Polynomfunktionen)
  • Daher ist zwischen zwei Wendestellen die Krümmung immer entweder positiv oder negativ … einfach einen beliebigen Wert aus diesem Bereich nehmen und f“(x) ausrechnen (lassen)
• Die Algebra-Befehle Extremum und Wendepunkt funktionieren nur bei Polynomfunktionen immer!
  Daher muss man z.B.: die Extremstellen bei Extremwertaufgaben in der Regel mit f’=0 und f“<>0 berechnen!
  Die Ableitung muss dann mit dem Befehl Nullstelle(A'(x),2) gelöst werden … A‘ wäre die Ableitung der Hauptfunktion, 2 der Startwert (also x-Wert in der Nähe des vermuteten Maximums/Minimums)
• Nullstelle bzw. Nullstellen sind bei Nicht-Polynomfunktionen ebenfalls nicht ganz so einfach: Bei Nullstelle muss man einen Startwert eingeben, bei Nullstellen wird nur der sichtbare Bereich untersucht (bzw. man gibt die Grenzen händisch an).
  Hier ist es sinnvoll Nullstellen zu verwenden, da alle Nullstellen ausgegeben werden.
  Wenn man das Intervall großzügig wählt, findet man auch alle!