Bei gegebener Wahrscheinlichkeit bzw. gegebenem Anteil wird die Grenze gesucht.
Beispiel:
Die Baumhöhe in einem Wald ist normalverteilt mit dem Erwartungswert von 25m und der Standardabweichung von 3m.
a) Gib die Höhe an, die 80% der Bäume überragen!
b) Gib die Baumhöhe an, ab der Bäume zu den kleinsten 20% gehören!
c) Gib die Baumhöhen an, zwischen denen die Bäume zu den mittleren 40% gehören!
Lösung a)
Im TR gibt es unter dem Punkt stat-reg/distr den Punkt 3 invNormal, welcher bei diesem umgekehrten Rechengang verwendet wird:

Da der TR immer die Fläche links von der Grenze nimmt, muss man statt 80% der größten Bäume 20% der kleinsten Bäume ansetzen, also mit dem gegensätzlichen Teil (analog zur Gegenwahrscheinlichkeit) arbeiten.
Zuerst muss man die Fläche = Anteil = Wahrscheinlichkeit angeben, also 0.2 = 20%.
Danach wieder die Kenngrößen Mean (Erwartungswert) und Sigma (Standardabweichung):

Das Ergebnis ist 22.4751363

Antwort: Ab einer Höhe von ca. 22,48 m gehört ein Baum zu den höchsten 80 % der Bäume des Waldes.
Lösung b)
Diese Fragestellung ist die gleiche wie in a), kann aber direkt gerechnet werden.
Antwort: Ist ein Baum kleiner als 22,48 m, so gehört er zu den kleinsten 20% der Bäume des Waldes.
Lösung c)
Hier muss man ein wenig rechnen:
Man möchte einen symmetrisch zum Erwartungswert liegenden Bereich, der 40% der Fläche ausmacht:
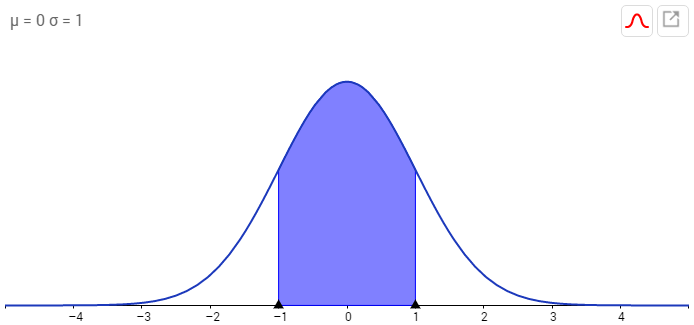
Der TR gibt aber nur Flächen links einer Grenze an.
Man überlegt sich daher, wie groß die linke, weiße Fläche unter der ersten gesuchten Grenze ist:
Der mittlere Bereich soll ja 40 % = 0,4 sein, daher bleiben für die beiden äußeren weißen Bereiche zusammen 60 % = 0,6.
Da die Flächen und die Grenzen symmetrisch liegen, bleiben für jeden der beiden weißen Bereiche die Hälfte, also 30% = 0,3.
area = 0.3 gibt uns also die erste Grenze.
Für die zweite Grenze spiegelt man entweder die erste Grenze auf die andere Seite vom Erwartungswert oder man zählt die unteren beiden Flächen zusammen (0,3 + 0,4 = 0,7) oder man rechnet 100% minus den oberen 30% und erhält ebenfalls 70% = 0,7.