Die Normalverteilung muss bei der Modellbildung in den meisten Fällen angepasst werden: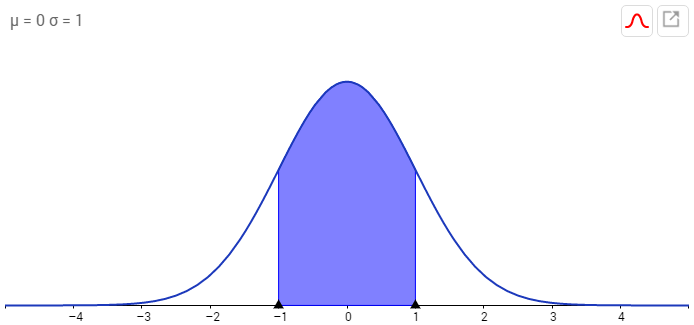



Die Glockenkurve wird mit ihrem Maximum in den Erwartungswert geschoben und entsprechend der Standardabweichung gestaucht oder gedehnt.
Mit Geogebra ist es kein Problem bei gegebenem Erwartungswert und Standardabweichung die Wahrscheinlichkeit für ein bestimmtes Intervall x1 bis x2 berechnen zu lassen.

Oft ist jedoch der Computer im Unterricht nicht mit dabei oder die Wahrscheinlichkeit ist gegeben und die Grenzen x1 und x2 müssen berechnet werden.
Hier hilft dann die Normalverteilungstabelle, die in beide Richtungen funktioniert (mit z-Werten die Wahrscheinlichkeit berechnen oder bei gegebener Wahrscheinlichkeit die Grenzen (z-Werte) ermitteln).

Die z-Transformations-Formel spielt dabei die zentrale Rolle: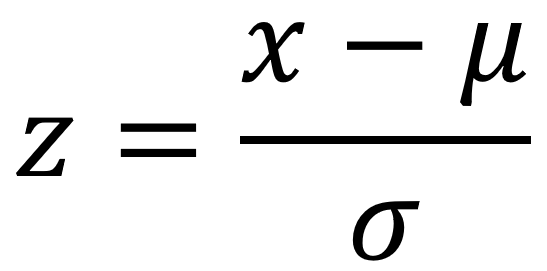

Mit dieser Formel kann zwischen den x-Werten des Modells (Grenzen im konkreten Beispiel) und den z-Werten (Grenzen in der Standardnormalverteilung) hin- und hergerechnet werden.

---

Beispiel:
Die Baumhöhe in einem Wald ist normalverteilt mit dem Erwartungswert von 17m und der Standardabweichung von 3,5m.
Berechne den Prozentsatz der Bäume, die
a) kleiner als 12m sind.
b) größer als 20m sind.
c) zwischen 15 und 19m sind.

Lösung a)
Mit Geogebra gibt man einfach die Werte ein: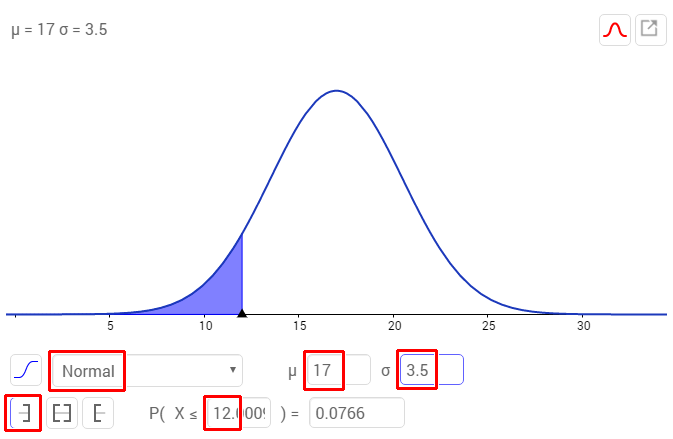

Man erhält hier die Wahrscheinlichkeit/Prozentsatz von 0.0766 = 7,66%.

Mit der Transormationsformel kann man die Grenze z berechnen:
z = (12-17)/3,5 = -1,4285
In der Tabelle sind nur positive Werte!
Man muss daher entweder in der Spalte für -z nachschauen, oder die Gegen-Wahrscheinlichkeit für den positiven z-Wert nehmen:
In der Tabelle nimmt man den Wert 1,43 (gerundet) und bekommt für die Wahrscheinlichkeit 0,0764 heraus.
Der Wert ist kleiner, da wir ja abgerundet haben (negativer Wert!).

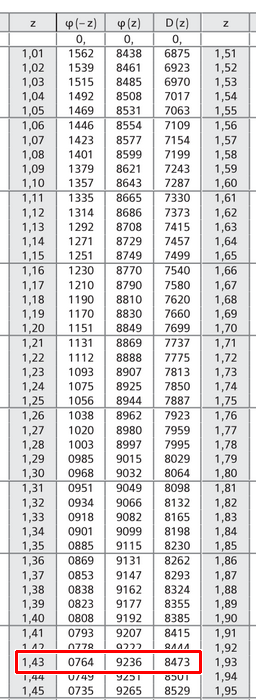
In manchen Tabellen ist nur Phi(z) abgedruckt. In diesem Fall nimmt man eben diesen Wert (also z mit falschem Vorzeichen) und liest die Gegenwahrscheinlichkeit 0,9236 aus der Tabelle aus.
Berechnet man von dieser Wahrscheinlichkeit wieder die Gegenwahrscheinlichkeit, so erhält man die gesuchte Wahrscheinlichkeit:
1 – 0,9236 = 0,0764

Graphisch schaut das wie folgt aus:

Die gesuchte Wahrscheinlichkeit Phi(-1,43):


Die Gegenwahrscheinlichkeit Phi(1,43):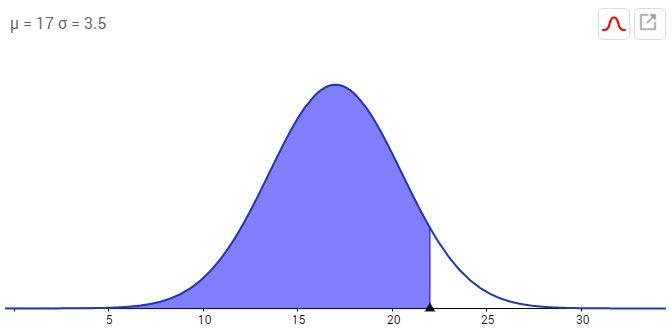

man sieht, dass das nur funktioniert, weil die Kurve symmetrisch ist.
(in der letzten Graphik ist die weiße Fläche gleich groß wie die blaue Fläche in der Graphik darüber).

Lösung b)

Die Lösung ist also 19,57%.

Mit der Tabelle muss man hier mit der Gegenwahrscheinlichkeit rechnen, da in der Tabelle nur die Flächen bis zum z-Wert abgelesen werden können – oder man nimmt wieder Phi(-z), was gleich das richtige Ergebnis liefert.
z = (20-17)/3,5 = 0,86
Aus der Tabelle bekommt man Phi(-0,86) = 0,1949 bzw.
1 – Phi(0,86) = 1 – 0,8051 = 0,1949 = 19,49%.

Lösung c)

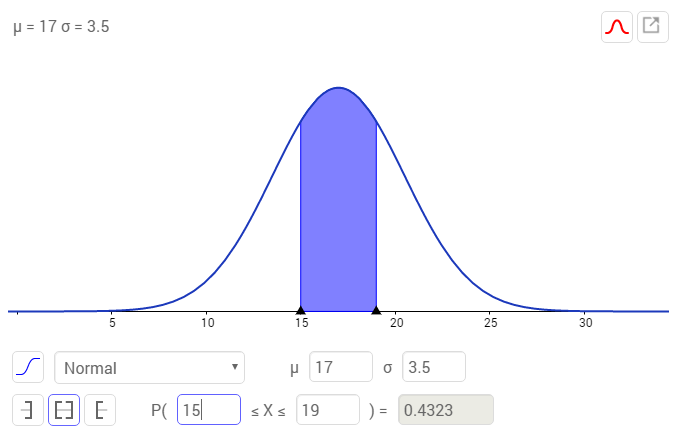
Lösung mit Geogebra: 43,23%

Möchte man mit der Tabelle die Fläche/Wahrscheinlichkeit zwischen zwei Werten berechnen, so liest man zuerst die Wahrscheinlichkeiten <=z aus und subtrahiert die Flächen so, dass die gesuchte Fläche übrig bleibt:
z1 = (15-17)/3,5 = -0,57 … Phi(-0,57) = 0,2843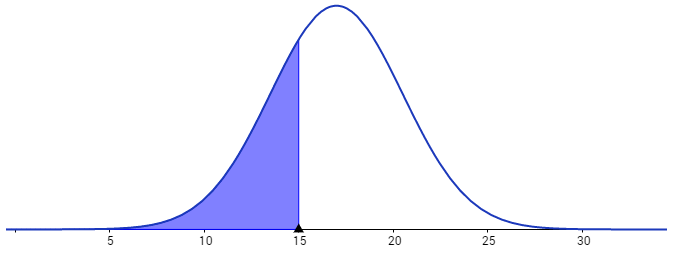

z2 = (19-17)/3,5 = 0,57 … Phi(0,57) = 0,7157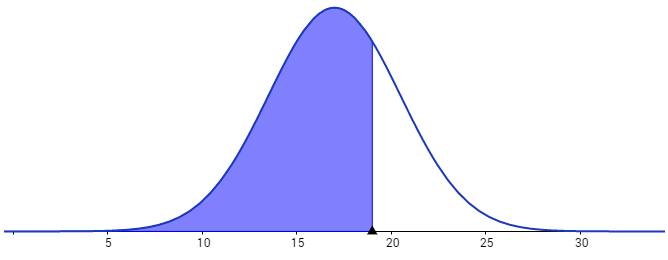

Die gesuchte Wahrscheinlichkeit ist somit die Subtraktion der unteren und der oberen Fläche: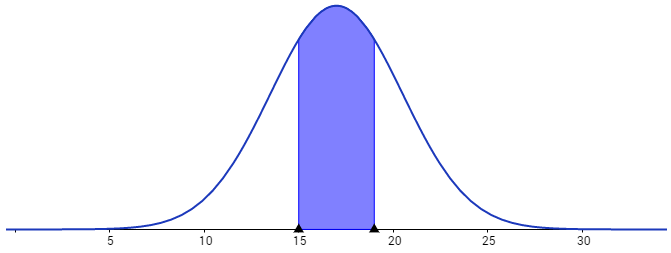

0,7157 – 0,2843 = 0,4314 = 43,14%