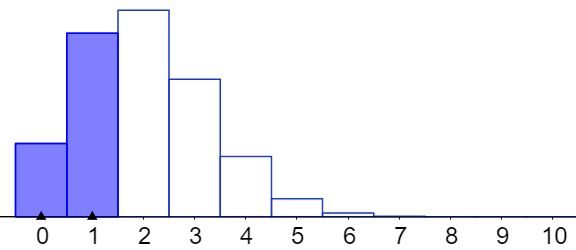
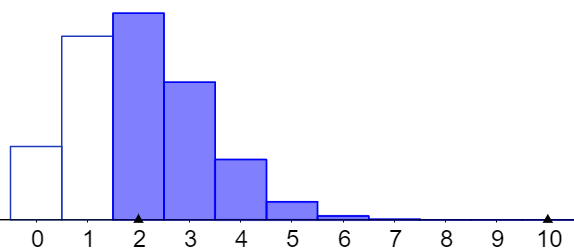
Hier ist ein Beispiel, wo man nicht blind drauflos rechnen sollte.
Rechnen kann man hier auch nicht viel (es steht NICHT da, dass es sich um eine Binomialverteilung oder ähnliches handelt, daher sind die restlichen Wahrscheinlichkeiten gar nicht berechenbar!)

Hier ist die Lösung einfach:
Da für n=10 die Wahrscheinlichkeiten P(X=0) und P(X=1) gegeben sind, aber die Wahrscheinlicheit für P(X>=2) gefragt ist, P(X>=2) aber die Summe aller restlichen Wahrscheinlichkeiten P(X=2) + P(X=3) + … + P(X=10) ist, kann man einfachP(X>=2) = 1 – ( P(X=0) + P(X=1) ) rechnen:
P(X>=2) = 1 – (0,35 + 0,38) = 0,27
Man kann auch sagen, dass P(X>=2) die Gegenwahrscheinlichkeit von P(X<=1) ist.

Die folgenden Graphiken sind von den Werten her nicht passend, sondern dienen nur dem besseren Verständnis der Zusammenhänge)