Pool 2_052d
Matura Wi201920 – Typ 1 – Bspl.12

Grundlagen zur Lösung sind hier zu finden:
Lösung
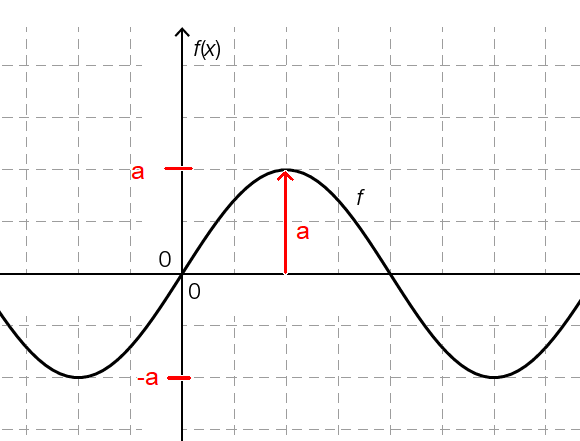
Die Amplitude a ist bei Winkelfunktionen am größten Ausschlag erkennbar (Abstand x-Achse zu größtem Mittelwert bzw. halber Max-Min-Wert/Spitze-Tal-Wert gilt auch bei in y-Richtung verschobenen Funktionen).
Der Wert 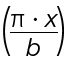 ist etwas schwieriger.
ist etwas schwieriger.
Ich empfehle hier wirklich zuerst obiges Video anzuschauen, dann ist die folgende Erklärung leicht zu verstehen:
x ist ja die Variable, also geht es eigentlich um den Parameter pi/b.
Wir (sollten) wissen, dass an dieser Stelle die Winkelgeschwindigkeit (Winkel/Zeit bzw. Winkel/x) steht.
pi/b ist also die Winkelgeschwindigkeit w.
Die Frequenz f = w/(2*pi) = (pi/b)/(2*pi) = pi/(2*b*pi) = 1/(2*b)
Hier könnte man also schon sage, dass 1 Schwingung 2b benötigt (oder 1/2 Schwingung in b, was auch mit der Periodenlänge P = 1/f = 2*b übereinstimmt:

Einleitung Testen von Hypothesen 02
M82 – Einleitung zu Testen von Hypothesen
Bitte den Einleitungstext zu diesem Thema lesen!
M82 – Fernunerricht aufgrund Covid-19
Aufgrund des Fernunterrichts arbeiten wir derzeit mit Microsoft Teams:
Bitte die Software herunterladen (Gibt sie für PC, Mac, Android, …)
https://teams.microsoft.com/downloads
Schul-Accounts verwenden (Schulemail-Adresse + Schul-PW).
- Jeder Schüler muss mit MS-Teams arbeiten – bei Problemen bitte eMail an mich!
- Es werden 2x in der Woche Beiträge/Aufgaben in MS-Teams bereitgestellt, die Abgabetermine der Aufgaben sind Mi und Fr.
Fragen können im jeweiligen Wochen-Kanal gestellt werden. - Aufgaben sind termingerecht(!) wie beschrieben zu bearbeiten und werden benotet!
- Bitte die Chat-Funktion sinnvoll und sparsam verwenden, da es sonst schnell unübersichtlich wird.
- Alles, was das Team/Klasse nicht erfahren soll/muss bitte mit einer PN per Schul-eMail oder Einzel-Chat (MS-Teams) an mich senden.
M82 – Normalverteilung
Benotung Schularbeiten 7./8. Klasse u. Matura

Die standardisierte schriftliche Reifeprüfung in Mathematik (pdf)
Grundkompetenzen, Benotungsschema, Antwortformate
