Grundlagen zur Lösung sind hier zu finden:

• Video „Material M62 – Die verflixte Zeitachse“
• Tafelbild „Tafelbilder M62 – 2018-02-23“

Lösung

Die Amplitude a ist bei Winkelfunktionen am größten Ausschlag erkennbar (Abstand x-Achse zu größtem Mittelwert bzw. halber Max-Min-Wert/Spitze-Tal-Wert gilt auch bei in y-Richtung verschobenen Funktionen).

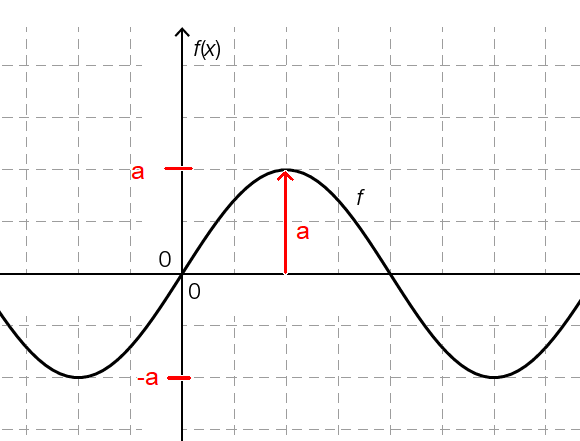
Der Wert 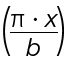ist etwas schwieriger.
Ich empfehle hier wirklich zuerst obiges Video anzuschauen, dann ist die folgende Erklärung leicht zu verstehen:
x ist ja die Variable, also geht es eigentlich um den Parameter pi/b.
Wir (sollten) wissen, dass an dieser Stelle die Winkelgeschwindigkeit (Winkel/Zeit bzw. Winkel/x) steht.
pi/b ist also die Winkelgeschwindigkeit w.
Die Frequenz f = w/(2*pi) = (pi/b)/(2*pi) = pi/(2*b*pi) = 1/(2*b)
Hier könnte man also schon sage, dass 1 Schwingung 2b benötigt (oder 1/2 Schwingung in b, was auch mit der Periodenlänge P = 1/f = 2*b übereinstimmt: